


suivant: À propos de ce
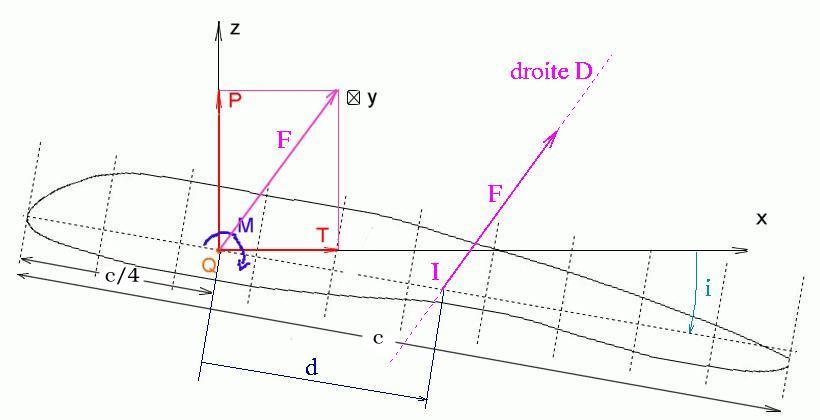
Considérons un profil d'aile subissant un vent
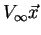 (suivant
(suivant 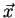 ).
L'action de l'air (de masse volumique
).
L'action de l'air (de masse volumique 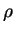 ) sur ce profil se résume, au point
) sur ce profil se résume, au point 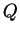 , à :
, à :
- une trainée (suivant
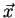 ) notée
) notée
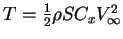 ,
,
- une portance (suivant
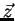 ) notée
) notée
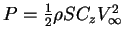
- et un moment (suivant
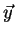 ) définit au point
) définit au point 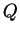 noté
noté
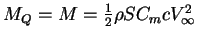 .
.
où 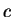 est la corde du profil et
est la corde du profil et 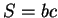 est une surface caractéristique de l'aile (
est une surface caractéristique de l'aile (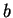 est sa largeur suivant
est sa largeur suivant 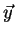 ).
).
 Le point
Le point 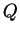 est définit arbitrairement (ou plutôt historiquement) : il est au 1/4 du bord d'attaque sur la corde (droite passant par les bords d'attaque et de fuite). Il est nommé le foyer du profil.
est définit arbitrairement (ou plutôt historiquement) : il est au 1/4 du bord d'attaque sur la corde (droite passant par les bords d'attaque et de fuite). Il est nommé le foyer du profil.
Il existe un point 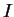 (à vrai dire le point
(à vrai dire le point 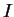 n'est pas unique car il se situe sur une droite
n'est pas unique car il se situe sur une droite 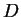 ) où le moment est nul
) où le moment est nul 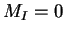 : le point
: le point 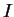 est nommé centre de poussée du profil.
Notons
est nommé centre de poussée du profil.
Notons 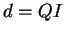 la valeur algébrique permettant de positionner
la valeur algébrique permettant de positionner 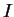 relativement à
relativement à 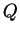 .
Nous avons la relation de transport des moments de torseur qui permet de déterminer la position d'un point
.
Nous avons la relation de transport des moments de torseur qui permet de déterminer la position d'un point 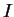 :
:
On a donc la position du centre de poussée 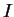 par rapport au foyer
par rapport au foyer 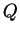 :
:
ou par rapport au bord d'attaque :
Il existe "mathématiquement" un angle 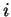 qui sera tel que
qui sera tel que
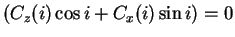 .
.
La fraction précédente ne sera pas définit où plutôt 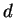 deviendra infini !
deviendra infini !
Ceci est illustré par le cas de figure suivant :
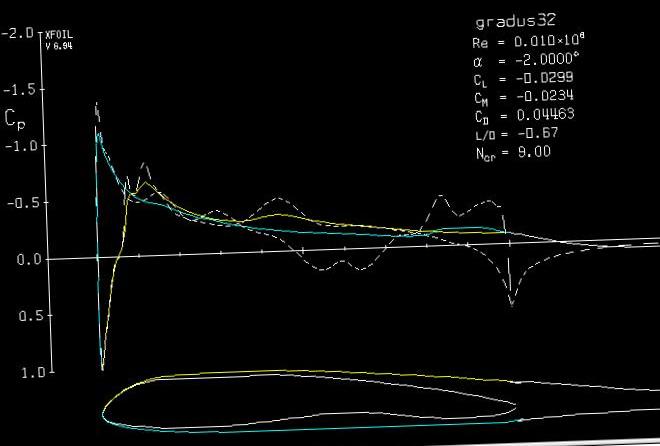
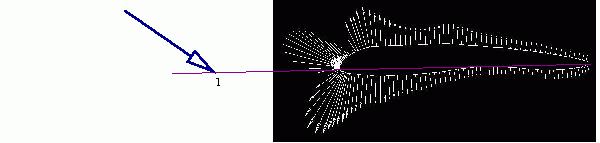 La répartition de force équivaut ici à une force appliquée en un point extérieur au profil.
La répartition de force équivaut ici à une force appliquée en un point extérieur au profil.
Il y a en effet aucune raison pour que le point 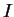 soit situé entre les bords d'attaque et de fuite du profil !
soit situé entre les bords d'attaque et de fuite du profil !
Si
![$(0.25 + \frac d c) \in [0;1]$](img24.png) , ce centre de poussée
, ce centre de poussée  est situé entre les bords d'attaque et de fuite du profil sinon il est en dehors !
est situé entre les bords d'attaque et de fuite du profil sinon il est en dehors !
Hypothèses et Simplification
En se référençant à des ouvrages aérodynamiques dont "Comment le planeur vole" de R.Gougnot (2002) ...
La force de trainée  étant plus faible que celle de portante
étant plus faible que celle de portante 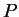 et l'angle d'incidence
et l'angle d'incidence 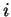 étant petit on a :
étant petit on a :
La formule précédente devient :
L'angle 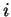 étant faible
étant faible
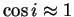 donc :
donc :
En considérant que le coefficient de moment évolue que très faiblement et en prenant la valeur de ce coefficient lorsque  :
:
On a la position du centre de poussée pris à partir du bord d'attaque qui sera approximativement donnée par :
Application sur quelques profils
Les équations précédentes sont programmées dans ces fichiers Fortran poscp.f et bdforce4.f
Travail étudiant sur quelques profils



suivant: À propos de ce
Laurent Blanchard
2007-02-02

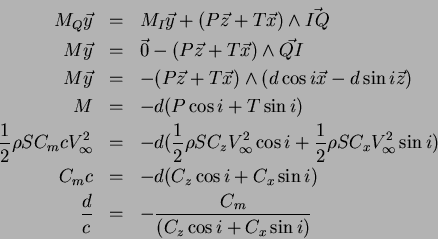
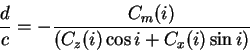
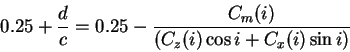
![]() qui sera tel que
qui sera tel que
![]() .
.
![]() deviendra infini !
deviendra infini !


![]() étant plus faible que celle de portante
étant plus faible que celle de portante ![]() et l'angle d'incidence
et l'angle d'incidence ![]() étant petit on a :
étant petit on a :