Méthodes numériques

Université Rennes1
Campus de beaulieu
UFR Mathématiques

 Informations sur le déroulement
  • Dates prévues pour les contrôles continus :
    • CC1 (1h) : Mardi 4 octobre 2016.
    • CC2 (1h) : Mardi 25 octobre 2016
    • CC3 (1h) : mardi 22 novembre 2016.
    • ECC (2h) : mardi 6 décembre 2016 de 14h à 16h en salle 305 du bâtiment 2.
  • Conférences sur les métiers d'ingénieurs calcul :

Documents à télécharger à partir de votre ENT : La formation > Mes cours en ligne
 Objectifs

Acquérir les compétences nécessaires pour résoudre numériquement des systèmes linéaires ou non linéaires, des problèmes d’équations différentielles ordinaires, calculer numériquement des intégrales, représenter des fonctions.
Apprendre à utiliser ses compétences mathématiques pour résoudre des problèmes concrets.
 Public visé

Tout étudiant de Master 1 s'intéressant aux applications des mathématiques et aux méthodes numériques avec en particulier :

  • les étudiants s'orientant vers les spécialités professionnelles du Master (Mathématiques de la Modélisation et Calcul Scientifique; Statistique - Économétrie; Mathématiques de l'Information - cryptographie),
  • les étudiants souhaitant présenter l'épreuve de modélisation au concours de l'Agrégation.
 Programme (24h de cours, 36h de TD/TP)
  • Recherche des zéros (dichotomie, Newton).
  • Calculs d’intégrales (interpolation, méthodes de Gauss, méthodes de Monte-Carlo)
  • Quelques algorithmes sur les matrices (factorisations, conditionnement)
  • Équations différentielles (théorie et numérique)
  • Approximation de fonctions (interpolation, splines,...)
  • Extrapolation à la limite (Richardson, accélération de la convergence).
  • Introduction à la méthode des différences finies (Dimensions 1 et 2).
 Illustrations

Pourquoi le résultat donné par l'ordinateur n'est-il pas toujours juste ? Cela vient souvent d'une erreur de programmation mais pas toujours :

  • Expérimentation de l'erreur d'arrondi dans une opération : soit x = 1 + 10n , y = 10n et z = x - y. Pour une arithmétique à 15 chiffres significatifs (double précision)

z = 1 pour n entre 0 et 15, mais z = 0 pour n > 15.

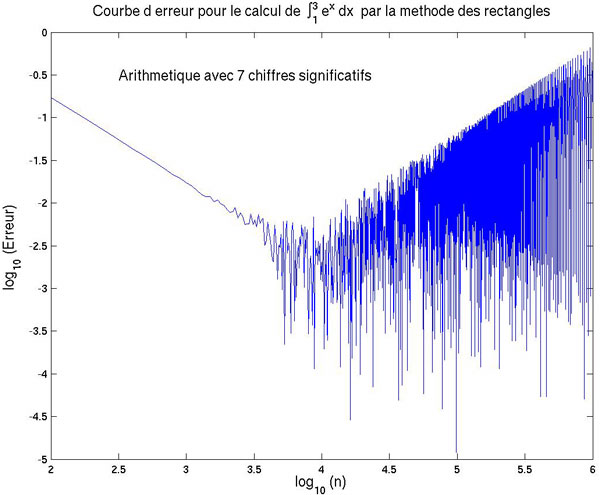
  • Effet du cumul des erreurs d'arrondis sur les résultats de l'intégration numérique de exp(x) entre 1 et 3 par la méthode des rectangles. Soit n le nombre de subdivisions, l'erreur de la méthode se comporte comme 1/n, c'est-à-dire qu'elle tend vers 0 linéairement quand n tend vers l'infini. Hors, numériquement on obtient cette convergence jusqu'à ce que le cumul des erreurs d'arrondis dépasse l'erreur de la méthode. C'est ce que l'on voit sur les graphiques superposés suivants pour une arithmétique à 7 chiffres significatifs (simple précision) et 15 chiffres significatifs (double précision) :
 Bibliographie

Analyse numérique

  • Approximation, intégration et équations différentielles : Analyse numérique des équations différentielles, M. Crouzeix, A.L. Mignot, Masson, Paris, 1989.
  • Méthodes numériques pour le calcul scientifique, A. Quarteroni, Collection IRIS, Springer, 2000.

Matlab

  • Analyse numérique avec Matlab, Jean-Louis Merrien, Dunod, Paris, 2007.
  • Introduction à l'analyse numérique - Applications sous Matlab, J. Bastien et J.-N. Martin, Dunod, Paris 2003.

Dernière mise à jour : 19/6/16 par Fabrice Mahé