Organisation du module H13 :
cliquez ici (emploi du temps - contrôle des connaissances -
...).
Présentation du module H13 :
* Objectifs
* Descriptif
* Références bibliographiques
* Prérequis
* Illustration
Objectifs :
Présenter les bases de
l'optimisation et étudier les principales méthodes numériques d'optimisation ainsi que leurs
applications.
Descriptif :
* Outils utiles à la mise en place des méthodes
d'optimisation : calcul différentiel dans les espaces de Hilbert (gradient - Hessien) ;
introduction à la topologie faible (convergence faible) ; convexité
d'une fonctionnelle définie sur un espace de Hilbert.
* Définition d'un
problème d'optimisation. Conditions nécessaires et suffisantes
d'optimalité.
* Algorithmes de calcul :
- Méthodes du gradient optimal,
du gradient à pas constant, du gradient conjugué (cas sans contrainte), Méthode
de la plus grande pente (cas avec contrainte).
- Méthodes de Newton, Multiplicateurs de Lagrange (cas
avec contraintes).
- Relations de Kuhn-Tucker, dualité, point-selle, algorithme
d'Uzawa (programmation non linéaire).
* Applications : contrôle
optimal d'équations aux dérivées partielles, problème inverse,
optimisation de forme, commande optimale.
Références bibliographiques :
** P.G. Ciarlet, Introduction à l'analyse numérique
matricielle et à l'optimisation.
Masson, 1989
** J. Céa, Optimisation, théorie et
algorithmes.
Dunod, 1971
** J.B. Hiriart-Urruty, L'optimisation.
Que sais-je ? P.U.F., 1996
Prérequis :
Des notions de calcul différentiel sont essentielles
(différentiabilité - dérivées partielles - gradient -
théorème des fonctions implicites).
Des notions en analyse fonctionnelle sont aussi conseillées (espaces de Hilbert -
convergence faible)
Illustration :
Les méthodes du gradient représentent une partie
conséquente de l'enseignement de ce module. Elles sont d'une grande efficacité pour la résolution de certains types
de problèmes d'optimisation. Itératives, on les appelle aussi "méthodes de descente" car elles sont basées sur le choix de la
plus grande pente à chaque itération. Plus précisément, à chaque itération, on se
déplace vers un nouveau point en lequel la fonctionnelle à minimiser sera plus petite. Ce déplacement s'effectue
selon une direction basée, entre autres, sur la direction de plus grande pente.
Imaginons que je suis à la montagne, en altitude, désirant redescendre
au fond de la vallée,
à travers une épaisse forêt avec un visibilité à faible distance.
Je pourrais alors décider le déplacement suivant : Au point où je me trouve, je prends la direction de plus grande
descente et je suis cette direction sans changer de cap jusqu'à arriver au point où la pente cesse de descendre et
s'apprête à devenir montante. A ce moment, je m'arrête et je réitère le procédé.
Après un certain temps, je devrais ne plus être très loin du point le plus bas de la vallée. C'est ce
que l'on appelle la méthode du gradient à pas optimal.
Un TP permettra aux étudiants d'étudier
d'un point de vue pratique la convergence de la méthode du
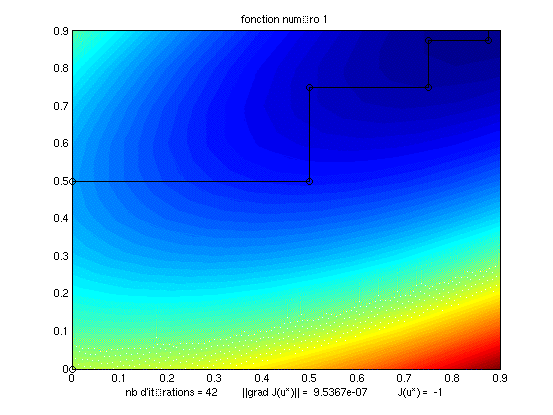
gradient à pas optimal vers le minimum de la fonctionnelle étudiée. Ci-dessous, nous montrons le déplacement
(en trait noir) que suit la méthode avant d'atteindre le minimum de la fonctionnelle, à une erreur près de l'ordre
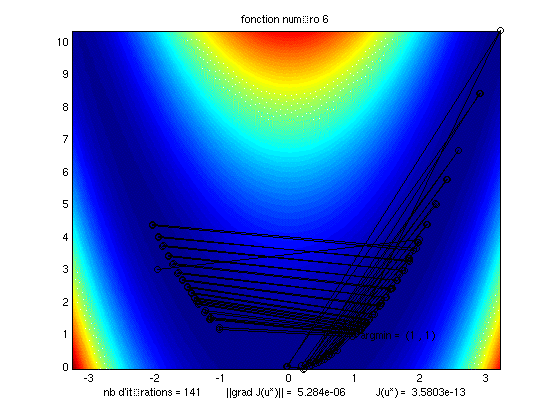
du millième. Les couleurs correspondent aux isovaleurs de la fonctionnelle. A gauche, la fonctionnelle ne présente
qu'une vallée bien profilée. La méthode converge très rapidement. Par contre, à droite, il s'agit d'un
cas avec deux vallées. La méthode converge difficilement et parfois diverge selon le choix du point de départ.
|
|
|
|
|
|
Lors d'une vallée unique
|
Cas à plusieurs vallées
|
Une application de ces méthodes sera abordée à la fin du cours :
La résolution du problème de propagation d'ondes électromagnétiques en domaine
extérieur, autour d'un obstacle (ex : un avion dans le ciel), est particulièrement difficile de par le caractère non borné du domaine.
Sous certaines conditions, un outil particulier, les formulations intégrales permettent de se ramener à
un problème en domaine borné : La connaissance
du champ diffracté dans l'espace tout entier est donnée par la connaissance des courants électromagnétiques
sur la surface de l'obstacle. Le nouveau problème consiste alors à déterminer les courants
électromagnétiques sur la surface de l'obstacle. Ceci se fait par la résolution d'équations dites
intégrales.
Plusieurs variantes de ces équations conduisent souvent à des systèmes mal conditionnés. Cependant, B.
Després a développé une nouvelle version de ces équations intégrales aux propriétés
remarquables.
Les équations intégrales de B. Després sont
établies par l'introduction d'un multiplicateur de Lagrange. La justification de l'existence et de l'unicité de la solution
de cette nouvelle formulation se fait par la théorie du point-selle étudiée dans ce cours. Après
discrétisation, ces équations aboutissent à un système dont les propriétés permettent une
résolution efficace basée sur des méthodes du gradient enseignées dans ce module.

