ZOHOUR library

What is Zohour?
Zohour is a free Node-Based Adaptive 2D mesh algorithm, written in
Fortran 2003 and developped since March 2014 by Édouard Canot.
The current version is numbered 0.9.3 and dated 2025-05-13.
See "Recent news" at the bottom of this page...
Only nodes are added or removed, from an initial regular, set of squared cells.
Moreover, the cells of the mesh correspond to the Voronoi tessellation;
however there exist only 10 different cell shapes. The advantage of such a
mesh is that, for a transient problem, almost nodes remain fixed and
therefore very few interpolation is needed.
The adaptive algorithm is optimized, especially the computation of the hessian
scalar invariant.
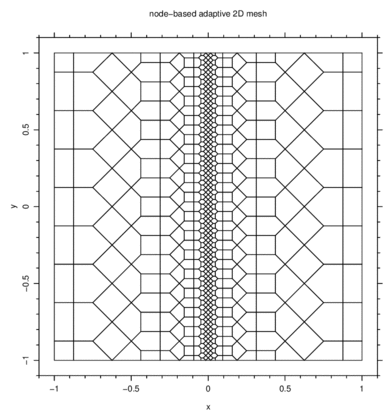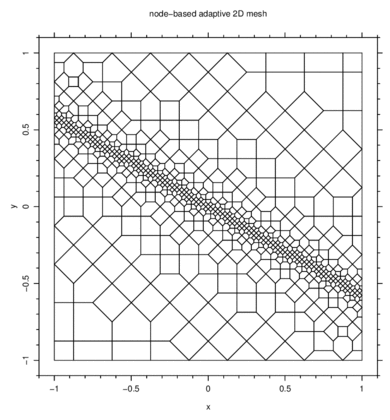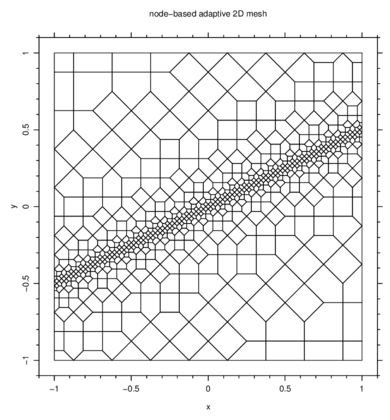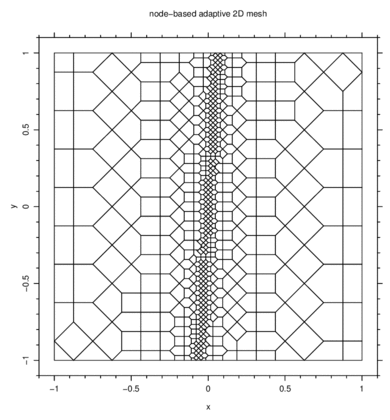
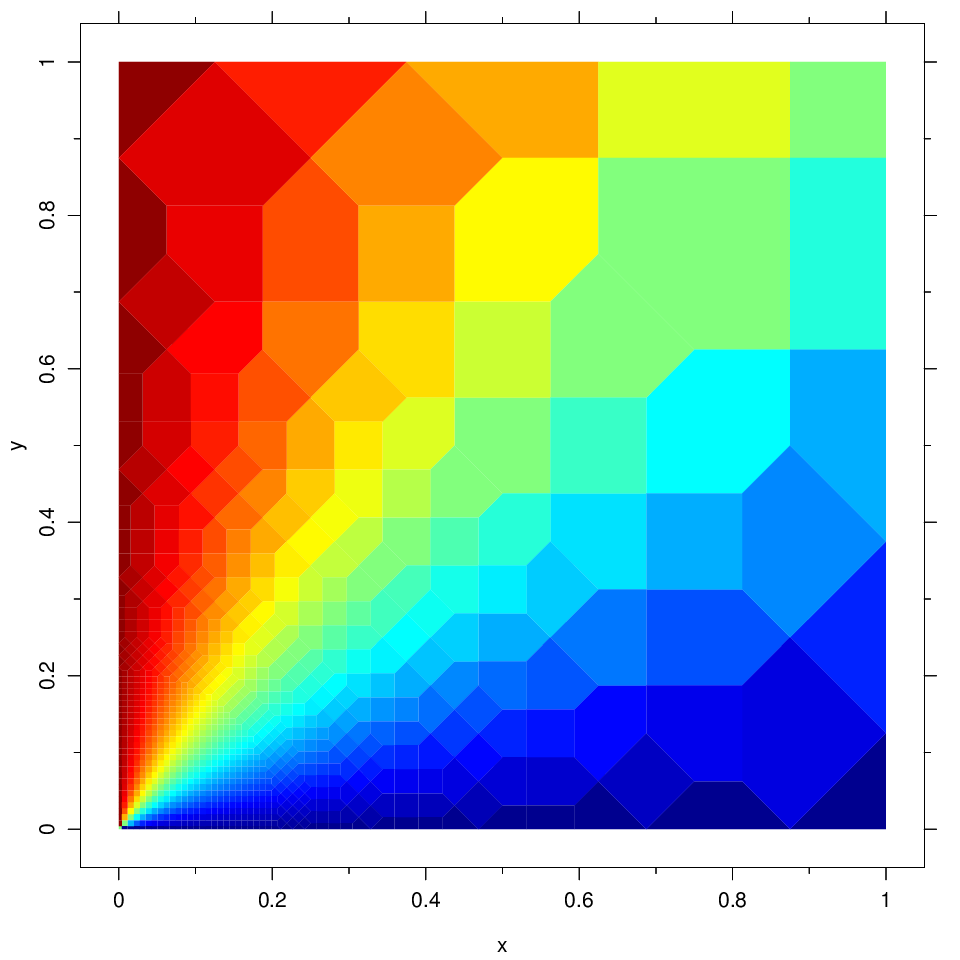
Excellent results are obtained when applying the meshing algorithm to a
strong singular laplacian problem (see the resulting mesh below):
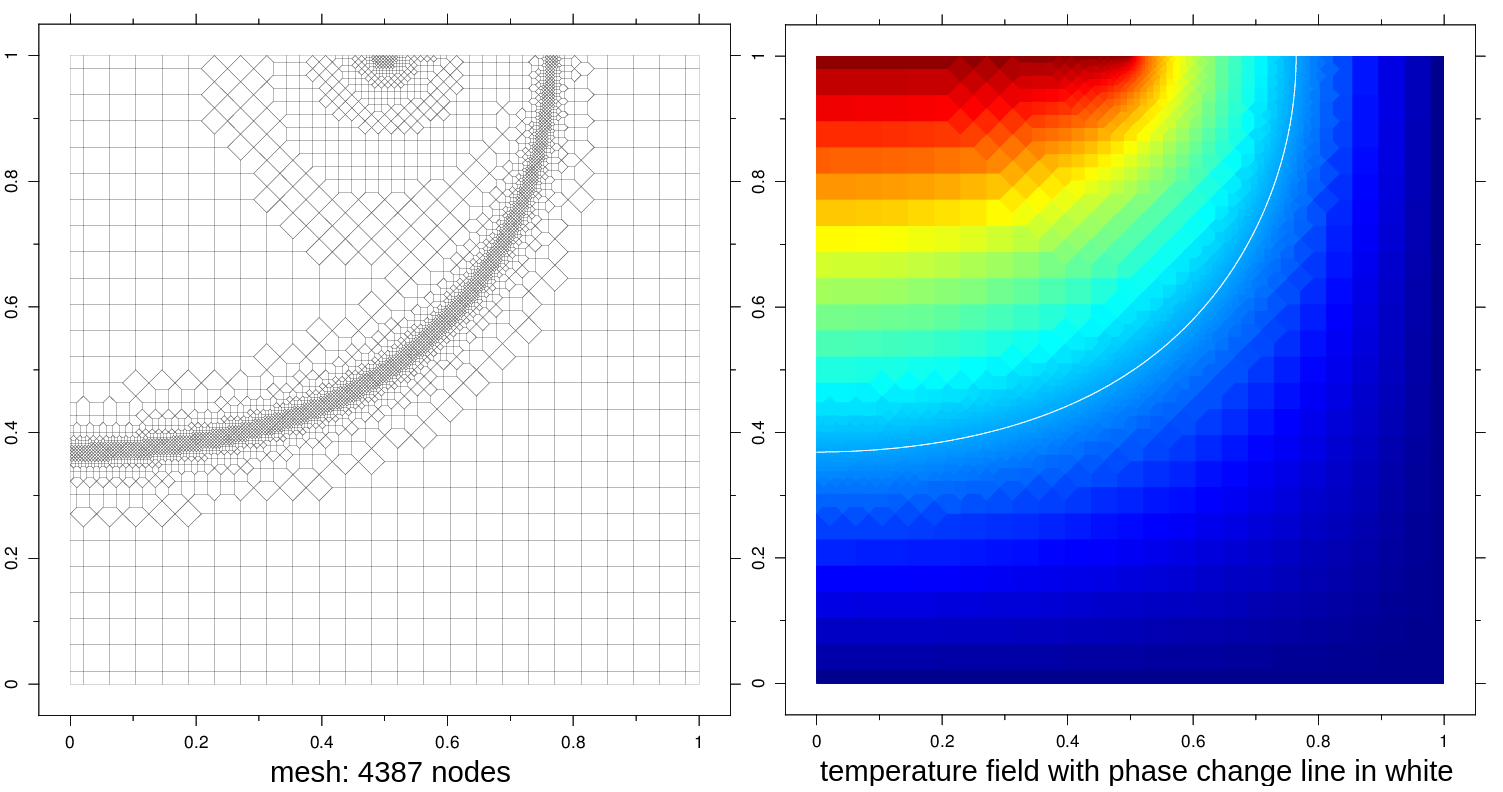
Another application shown below concerns the heat transfer with phase change,
across a 2D domain. The mesh has to be refined near the moving phase change
line, represented by the 100 °C isocontour line:
Please note that the Fortran compiler used to build Zohour must support
unlimited polymorphism (Fortran 2003 feature):
- GCC gfortran, version ≥ 4.8
- INTEL ifort, version ≥ 12 ? (release 14 is ok)
Documentation:
A short documentation about the main characteristics of Zohour:
Zohour_inside.pdf
(in french).
A User Guide of the library:
Zohour_user_guide.pdf (in english,
work in progress...)
Download:
Linux 64-bit binary files (compiled with different GNU Fortran releases)
can be found here.
You need both the archive library and the precompiled module file (the name
of the module is 'zohour_2d').
Note that you need the same compiler to use the precompiled binary module.
About the name:
Read this Document (in french).
Recent news:
- 2025-05-13: 0.9.3 version release. Few bugs fixed.
init_mesh routine improved. Recent releases of GCC (up to
15) are now supported.
- 2019-03-30: 0.9.1 version release. Cells signature is know
embedded in the cell data.
- 2016-01-20: Update concerning the 0.9.0 version. The domain can be now
rectangular. Each side of the domain may contain any number of different
boundary condition types, defined by the user.
- 2015-06-04: Update concerning the 0.8.6 version.
- 2014-04-04: Creation of the web page for the 0.8 version.
For any question, please contact the author:
Mail: 
Come back to the author web page.
Last page modification: 2025-05-28





