Krigeage

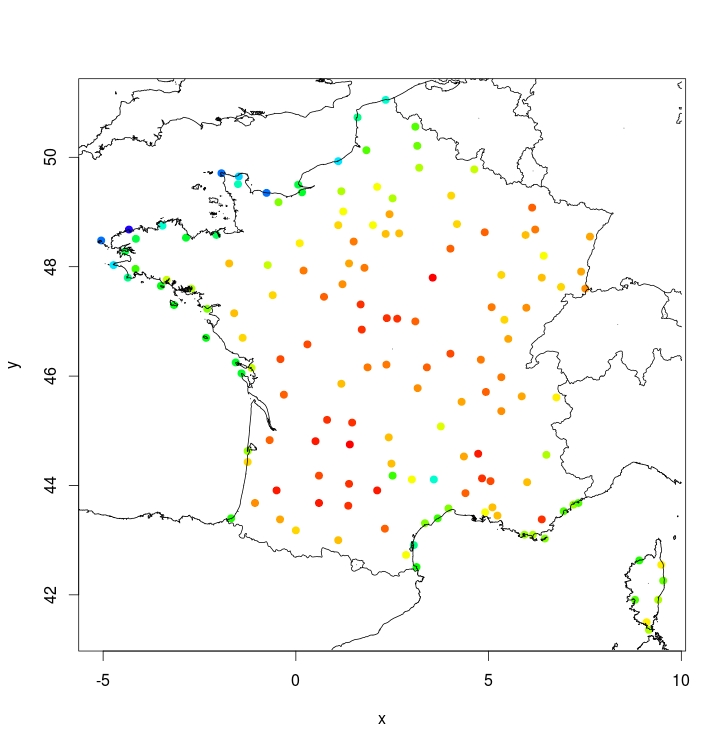
On dispose des températures dans 150 villes de France un jour de canicule en août 2003. Les trois variables sont
  • lat : latitude de la ville
  • long : longitude
  • data : température
L'objectif est de compléter ces données sur toute la France, ici sur une grille de points 100x100. Et en particulier d'estimer la température à Rennes (longitude=-1.7, latitude=48). 		  BD
On suppose que le processus des températures à cette date est un vecteur gaussien de moyenne m (indépendante de l'endroit) et de covariance

  Rvw =a exp(-  d(v,w)b)

où a et b sont des paramètres et d(v,w) est la distance entre les deux villes.
Cette modélisation est à peu près la plus simple qui soit.
L'objectif est donc

 (1) Estimer m, a, et b.
 (2) Prédire la température sur les autres villes en utilisant le modèle gaussien.

Description du TP

Programmes et données à charger:


Données de température. Données de frontière pour les tracés

Le programme principal, et des routines pour les tracés, les calculs de distance en fonction de longitude et latitude, et l'estimée non-paramétrique du covariogramme

Etude supplémentaire

On considère maintentant le modèle

  Rvw =a (p.exp(-  d(v,w)b) +(1-p)sin(d(v,w)/c)d(v,w)/c)

Il s'agit de procéder comme précédemment mais sur les fichier pluie et frontières qui concenent des mesures de précipitation au Paraná.
Noter que les variables north et east sont simplement des kilomètres, ce qui modifie le calcul des distances.

1/ Qu'est-ce qui motive l'introduction du terme sinusoïdal ?

2/ Faire l'étude (estimation et leave-one-out):
On prendra encore pour a et m les estimateurs des moments, et l'on optimisera sur (b,c,p).
L'estimation n'est pas facile, il faut une bonne valeur initiale pour (b,c,p) dans optim().
Pour le p initial on prendra 1/2.
Pour le b initial on pourra commencer par estimer le modèle sans sinus (p=1) ce qui conduit une valeur raisonnable de b.
Proposer enfin intelligemment une valeur initiale pour c, et estimer.
Noter que sin(x)/x vaut 1 si x=0.

3/ Discuter de l'opportunité d'avoir introduit le sinus et de la qualité des résultats.