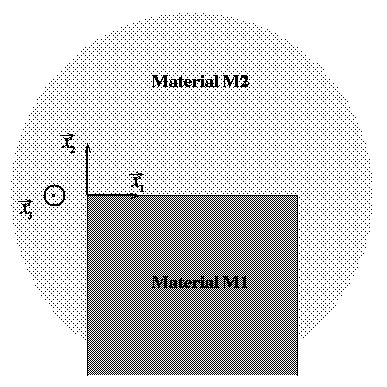
We consider the case of an orthotropic cylindrical object (material M1) plugged into an anisotropic one (material M2), as shown on the figure below. We assume that the upper part of the cylinder is free from the material M2, which corresponds to an internal crack. In this situation, we have Neumann boudary conditions on both sides of the interface.
The data file corresponding to the previous configuration is given below. The action chosen is to "turn" around the edge of the cylinder.
****** Every line starting with * is ignored. * Separate data values with a space or a new line. * Maximum length of a data line : 90 characters. ******************************************************************************* * Orthotropic cylindrical object plugged into an anisotropic one * Dimension of the space (2 or 3) 3 * Number of domains (K <= 4) 2 * ---> The domains are assumed to be numbered counterclockwise. * Context for each domain * in dimension 2 : * 1 : isotropic elasticity * 2 : axisymetric orthotropic elasticity (C11=C22) * 3 : orthotropic elasticity * 4 : general elasticity * in dimension 3 : * 1 : isotropic elasticity * 4 : general elasticity 4 4 * Cij coefficients for each domain. According to the context, give * in dimension 2 : * 1 : lambda mu * 2 : C11 C12 C66 * 3 : C11 C12 C22 C66 * 4 : C11 C12 C16 C22 C26 C66 * in dimension 3 : * 1 : lambda mu * 4 : the 21 coefficients in the following order : * C11... C16 C22... C26 C33... C36 C44... C46 C55 C56 C66 * material 1 (anisotropic) : 2.27000 0.522000 0.672000 0. 0. 0. 16.27000 0.272000 0. -0.3 0.1 10.5000 0. 1. 0. 0.485000 0. -0.1 0.485000 0. 0.324000 * material 2 (orthotropic) : 1.27000 0.622000 0.672000 0. 0. 0. 2.27000 0.672000 0. 0. 0. 14.5000 0. 0. 0. 0.485000 0. 0. 0.485000 0. 0.324000 * Angles (in degrees) defining the geometry of the domains, * that is omega(i), i = 0,...K 0 270 360 * Boundary conditions at omega(0) and omega(K) * 1 : Dirichlet * 2 : Neumann * 3 : Mixed normal Dirichlet - tangent Neumann * 4 : Mixed tangent Dirichlet - normal Neumann * 5 : Transmission 2 2 * Action to be done : integer 10*a1 + a0 such that * a0 = 0 (Manual computation), 1 (Automatic computation (= AC)), * 2 (AC + rotation of axes), 3 (AC + variation of the geometry) * 4 (AC + orientation of the materials), 5 (AC + edge tracking) * --> a0 = 2, 4 or 5 in dimension 3 only * a1 = 0 (Kernel not computed), 1 (Computation of the kernel of A(nu)) * 2 (1 + computation of the singular functions) 2 * Rectangular domain where to search for the roots (necessary if a0 > 0) * Give xmin xmax ymin ymax such that 0 < xmin < xmax and ymin < ymax. 0.1 1.2 -1. 1. ***************** Mutually exclusive specific actions ***************** * -> Do not modify the keyword "ACTIONi" that marks the beginning of data. * ACTION2 (a0 = 2 : Automatic computation + rotation of axes) * Definition of a rotation * 1) starting angle, end angle, step (in degrees) 0. 360. 1. * 2) number of the rotation axis 2
Running the program with this data file gives the exponents along the internal circular edge. They are shown on the following figure :
All the exponents are real. There are 6 exponents for each value of the angular parameter governing the computation. However, one can only see 5 curves on this graph. A zoom is needed to make the 6th curve appear : two exponents are very close, their difference is less than 1.e-3 as we can see on the following figure :
We present here the singular functions corresponding to the first 3 exponents computed for a rotation angle equal to 180 degrees. This can be easily obtained by modifying slightly the last part of the data file as follows :The graph of the singular functions are then :
. . . * Action to be done : integer 10*a1 + a0 such that * a0 = 0 (Manual computation), 1 (Automatic computation (= AC)), * 2 (AC + rotation of axes), 3 (AC + variation of the geometry) * 4 (AC + orientation of the materials), 5 (AC + edge tracking) * --> a0 = 2, 4 or 5 in dimension 3 only * a1 = 0 (Kernel not computed), 1 (Computation of the kernel of A(nu)) * 2 (1 + computation of the singular functions) 22 * Rectangular domain where to search for the roots (necessary if a0 > 0) * Give xmin xmax ymin ymax such that 0 < xmin < xmax and ymin < ymax. 0.1 0.6 -1. 1. ***************** Mutually exclusive specific actions ***************** * -> Do not modify the keyword "ACTIONi" that marks the beginning of data. * ACTION2 (a0 = 2 : Automatic computation + rotation of axes) * Definition of a rotation * 1) starting angle, end angle, step (in degrees) 180. 180. 1. * 2) number of the rotation axis 2
and the stress functions are :
| Summary |