(Texte faisant suite à l'article "Enfin un palindrome parfait ?" Quadratures 49)
DÉFINITION
On fait correspondre à chaque lettre son rang dans l'alphabet, ainsi A=1, B=2, etc..., Z=26. L'écart palindromique (EP) d'une expression de taille paire a1a2....a2n est alors donné par la formule :
EP
= 1/n ( |a1-a2n| +
|a2-a2n-1| +.... +
|an+an+1| )
De manière analogue, L'EP d'une expression de taille impaire a1a2....a2n+1 est donné par la formule :
EP
= 1/n ( |a1-a2n+1|
+ |a2-a2n| +.... +
|an-1+an+1| )
POINTS FIXES
Voici l'EP des vingt-six premiers entiers naturels, qu'on écrit sous la forme rationnelle irréductible.
| Zéro |
Un | Deux | Trois | Quatre | Cinq | Six | Sept | Huit | Neuf |
| 12 |
7 |
18 |
5 |
34/3
= 11,33... |
19/2
= 9,5 |
5 |
6 |
12 |
12 |
| Dix | Onze | Douze | Treize | Quatorze | Quinze | Seize | Dix-sept | Dix-huit | Dix-neuf |
| 20 |
11 |
6 |
9 |
39/4
= 9,75 |
22/3
= 7,333... |
35/2=
17.5 |
14 |
19/3
= 6,333... |
11 |
| Vingt | Vingt et un | Vingt deux | Vingt trois | Vingt quatre | Vingt cinq | ||||
| 2 |
7 |
13/2
= 6,5 |
3 |
39/5
= 7,8 |
19/4
= 4,75 |
Sachant que l'EP est compris entre 0 et 25, le seul point fixe entier est donc 11.
Par ailleurs, le rationnel 33 / 4 est un autre point fixe. En effet : l'EP de "Trente-trois / quatre" est bien 33 / 4
Question : Existe t-il d'autres points fixes rationnels ?
Question : Quel est le plus petit point fixe ? Le plus grand est-il égal à 11 ?
DÉVELOPPEMENT DÉCIMAL
O peut chercher des expressions dont l'EP, écrite sous forme de développement décimal, soit un palindrome numérique. Pour que cela ait un sens, il faut que l'EP soit un nombre décimal, sinon le développement décimal est infini périodique et il est donc difficile d'en comparer le début et la fin !
Bien évidemment l'EP de tout véritable palindrome est 0 qui est un palindrome numérique de taille 1, "Développement décimal " a un EP de 7,7 qui est un décimal de taille 2. De même, "Opérations " a un EP de 8,8 qui est un décimal de taille 2.
Citons encore "fonctions" dont l'EP vaut 5,25 qui est un palindrome numérique de taille 3.
Question : Trouver des expressions dont l'EP décimal est un palindrome numérique de plus long développement décimal possible.
ÉCART PALINDROMIQUE MAXIMAL
On s'intéresse aux expressions de taille N dont l'EP est "grande". On appelle EXP(N) (resp. exp(N)) la valeur maximale (resp. minimale) de l'EP d'une expression de taille N. De même, NOM(N) (resp. nom(N)) pour les noms communs, et NOMP(N) (resp. nomp(N)) pour les noms propres.
On se limitera bien entendu aux expressions ayant un sens, et correctes sur les plans de la syntaxe, la grammaire et l'orthographe.
Commençons par examiner les petites valeurs de N.
| N |
nom | NOM |
| 1 |
0
(a) |
0
(a) |
| 2 | 0 (aa) |
21
(va) |
| 3 |
0
(ici) |
23
(aux) |
| 4 | 0
(erre) |
22
(axez) |
| 5 |
0
(kayak) |
22
(axiez) |
| 6 |
0 (selles) |
19 (axerez) |
| ... |
||
| 21 |
59/10 (postsynchronisassions) |
10
(désembourgeoiseraient) |
| 22-23 24 |
0 |
0 |
| 25 |
29/4=7,25 |
29/4=7,25 |
La première colonne du tableau commence par une suite de zéros. Ceci est du au fait qu'il existe des mots palindromes de taille 1,2,3,4,5,6,7,8,9. Les mots palindromes les plus long comportent en effet 9 lettres (ressasser par exemple). La quantité nom(N) est donc non nulle à partir du rang 10 (sauf en ce qui concerne les cas N=22,23,24). Notons en effet qu'il n'existe pas de mot de 22 à 24 lettres, ce qui explique la valeur 0 de nom et NOM. Quant au rang 25, il est aisé à traiter car anticonstitutionnellement est l'unique nom de 25 lettres, qui réalise donc à la fois le minimum et le maximum de l'EP.
Question : Compléter et affiner le tableau précédent.
Question : Commencer un tableau analogue pour les expressions.
Question : Quelle est la valeur de limsup EXP(N) lorsque N tend vers l'infini ?
Je ne peux que vous inciter à aller consulter un site remarquablement fourni sur les palindromes (et fourmillant aussi de plein d'autres trouvailles) : http://www.fatrazie.com/palindromes.htm
LA SUITE DES ITÉRÉS
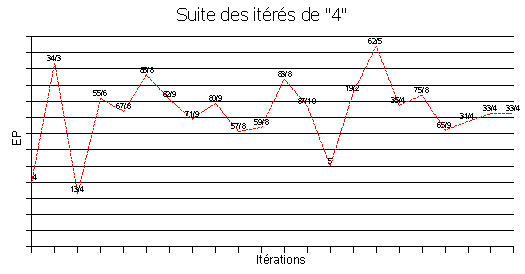
Les seuls suites d'itérés à valeurs entières sont nécéssairement de la forme (S1, 11, 11, ...) ou (S1, 19, 11, 11, ...). Il suffit pour s'en convaincre de remarquer que le second élément de la suite d'itérés est toujours compris entre 0 et 25.
L'immense majorité des exemples testés fournit une suite stationnaire vers 33/4 le point fixe attractif. Peu d'autres exemples stationne vers 11, point fixe répulsif, et dans ce cas la convergence se fait très rapidement, en une ou deux itérations.
Et il n'est apparu qu'une seule suite d'itérés non stationnaire en 11 ou 33/4. A savoir la suite (périodique) :
41/7,
33/8, 41/7,33/8....
Question : Existe t-il d'autres exemples de suites périodiques ou ultimement périodiques ?
Question : Existe t-il des suites d'itérés non périodiques et non ultimement périodiques ?
Par exemple, il serait intéressant de savoir s'il peut exister une suite convergeant vers 0, Ou alors possédant 0 comme valeur d'adhérence, i.e. une expression ultimement palindromique ?
AILEURS
En anglais, eight (8) et eleven (11 : encore lui !) dont points fixes pour l'EP.
Question : Sont-ils attracteurs, répulsifs ?
Plus près de chez nous, chez nos amis belges et suisses :
Question : L'apparition de septante, octante, et nonante génére t-elle d'autres phénomènes ?
On peut étudier d'une manière générale, les itérés quelle que soit la langue considérée.
Question : Est-ce qu'il existe qu'un nombre fini de points fixes, lesquels sont attracteurs, etc..