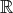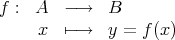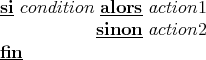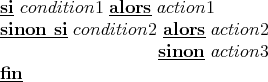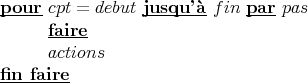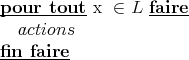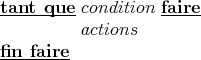Table des matières
-
![[dangerous l bend]](xsok0c7f.png) Ce document est conçu comme un recueil commenté d’exemples “simples” de
commandes Scilab . Il permet de découvrir l’existence de certaines commandes
Scilab et leur domaine d’utilisation, mais la lecture de ce document ne peut
remplacer la lecture de l’aide en ligne pour une utilisation optimale des commandes
décrites. Ce document est conçu comme un recueil commenté d’exemples “simples” de
commandes Scilab . Il permet de découvrir l’existence de certaines commandes
Scilab et leur domaine d’utilisation, mais la lecture de ce document ne peut
remplacer la lecture de l’aide en ligne pour une utilisation optimale des commandes
décrites. |
Scilab est un logiciel de calcul numérique, qui permet de manipuler la plupart des
objets mathématiques courants (nombres réels, booléens, matrices, fonctions, polynômes,
graphes,. . .). Scilab est aussi un logiciel libre (depuis la version 5) dont vous pouvez vous
procurer la dernière version sur le site de l’INRIA (Institut National de la Recherche en
Informatique et en Automatique) :
Vous
y trouverez les fichiers nécessaires pour l’installer sur n’importe qu’elle plate-forme (PC
WINDOWS™/UNIX ou MACINTOSH™) . Techniquement, Scilab est un interpréteur de
commandes, il se présente donc comme une calculatrice ou un shell : les commandes,
tapées à l’invite des commande ou lancées à partir d’un script, sont traduites dans un
autre langage (Fortran ou C), compilées, puis exécutées par le noyau du système
d’exploitation, le résultat (ou l’erreur) est récupéré par Scilab et affiché dans la
console.
dans la suite les exemples de code Scilab ou de sortie « console » apparaissent dans
des cadres gris-bleu alors que les remarques sur les erreurs et les confusions les plus
fréquentes apparaissent dans des cadres rouges :
-
![[dangerous l bend]](xsok0c7f.png) erreur fréquente . . . erreur fréquente . . . |
1 Prise en main de Scilab
Lorsque vous démarrez Scilab la fenêtre principale s’ouvre comme sur la figure FIG.1. Un
curseur apparaît juste après l’invite des commandes (-->) c’est à cet endroit que vous
pourrez lancer les lignes de commandes qui seront exécutées séquentiellement, de la
même manière qu’avec une calculatrice ou que dans une fenêtre xterm sous
linux. Pour pouvoir utiliser la console il faut comprendre les quelques règles
suivantes :
- chaque commande Scilab doit se terminer par
- un retour à la ligne (
 ), ce qui nous limite à une commande par ligne,
), ce qui nous limite à une commande par ligne,
- une virgule (,), ce qui permet de mettre plusieurs commandes par ligne,
- ou un point virgule ( ;) qui permet aussi d’exécuter plusieurs commandes par
ligne en bloquant l’affichage du résultat précédant le point virgule. Le point
virgule est très utile pour masquer le résultat d’un calcul intermédiaire.
- vous pouvez copier/coller des instructions avec la souris (mais pas modifier une ligne
de commande déjà exécutée)
- On peut rappeler les commandes précédemment exécutée en utilisant les touches du
curseur ↑ et ↓.
- dans une ligne tout ce qui suit un double slash (//) est ignoré (ce qui permet
d’insérer du commentaire).
- Scilab possède une aide en ligne accessible depuis la barre de menus, dans
l’onglet ?.
Vous pouvez aussi accéder à l’aide en ligne de Scilab directement depuis la console.
Pour cela il y a deux commandes différentes suivant le type de recherche qu’on veut faire
dans l’aide en ligne :
- help commande si vous voulez connaître ce que fait une commande dont vous
connaissez déjà le nom,
- apropos mot_clé si vous cherchez des commandes ayant rapport avec un
thème décrit par un mot_clé
Pour comprendre observez la différence de résultat entre les deux commandes :
-->help sin
-->apropos sinus
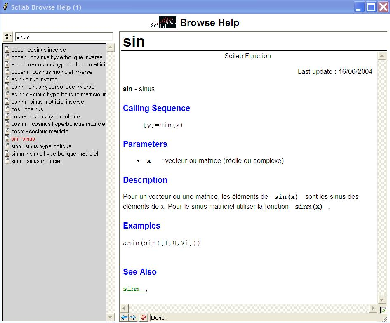
la première commande va trouver la page d’aide de la fonction sinus (sin en Scilab )
alors que la deuxième va renvoyer la liste des commande ayant un rapport avec la
fonction sinus (en fait la liste des fonctions trigonométriques comme sur la figure
FIG.2).
Une dernière chose importante qu’il faut comprendre pour bien travailler avec
Scilab c’est la notion derépertoire courant. On a souvent besoin avec Scilab d’importer
des informations, ou au contraire d’en exporter, et ceci à l’aide de fichiers. Lorsque c’est le
cas, Scilab va chercher à effectuer ces opérations avec les fichiers présents dans
son répertoire courant. Au démarrage de Scilab ce répertoire est le répertoire
depuis lequel Scilab a été lancé. Par exemple, sous windows™, ça peut être
C:\Program Files\Scilab-x.x.x\bin\ si vous démarrez Scilab depuis son répertoire
d’installation par défaut. Il existe plusieurs fonctions dédiées à la manipulation des
répertoire courant :
- Pour connaître le répertoire courant actuel : getcwd() ou pwd()
- pour changer de répertoire courant : cd() ou chdir()
- pour créer un répertoire (dans le répertoire courant actuel) : mkdir()
- pour lister le contenu du répertoire courant ls
Plus généralement, on peut aussi exécuter des commandes systèmes avec la fonction unix()
(la sortie pouvant être redirigé vers scilab ou pas).
-->getcwd() ans = C:\Program Files\Scilab-4.1.2\bin -->cd('C:/')
ans = C:\ -->ls ans = !temp !
! ! !Program Files ! ! !
!WINDOWS ! ! ! !Documents and Settings !
-->mkdir('scilab') ans = 1. -->chdir('scilab') ans =
0. -->pwd() ans = C:\scilab -->cd('..') ans = C:\
|
|
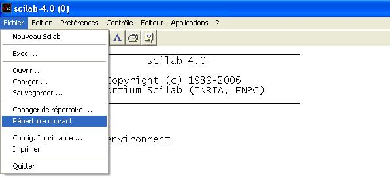
On peut aussi accéder à certaines fonctionnalités, comme changer ou afficher le répertoire
courant, à partir du menu fichier.
2 Les nombres en Scilab
Les objets de base du langage Scilab sont les nombres réels. Il sont représentés par des
nombres flottant double précision (i.e. avec un exposant signé et une mantisse d’environ
16 décimales), Scilab les affiche dans la console par défaut sous forme décimale avec 8
chiffres significatifs. Les opérations usuelles sur les réels sont codées de manière naturelle,
voici leur liste par ordre de priorité croissante :
|
|
|
|
|
| addition | soustraction | multiplication | division | puissance |
|
|
|
|
|
| + | - | * | ∕ | ^ |
|
|
|
|
|
| |
et on a en plus accès à la plus part des fonctions spéciales :
|
|
fonctions trigonométriques | sin(), asin(), cos(), acos(), tan(),
atan(), cotg() |
|
|
fonctions hyperboliques | sinh(), asinh(), cosh(), acosh(), tanh(),
atanh(), coth() |
|
|
fonctions d’arrondis | round(), int(), floor(), ceil() |
|
|
logarithme et exponentielle | exp(), log(), log10(), log2() |
|
|
autre | sqrt()(racine), abs() (valeur absolue),
pmodulo() (modulo) |
|
|
| |
,
Voici quelques manipulations de base :
-->1+2 ans = 3. -->2*3 ans = 6. -->1/3
ans = 0.3333333 -->1/4;sin(1) ans = 0.8414710
-->2^(1/2),sqrt(2) ans = 1.4142136 ans = 1.4142136
|
|
Notez qu’un nombre en Scilab contient toujours le caractère “.”, y compris les nombres
entiers (même si le point est facultatif lors de la saisie).
Les constantes, comme e et π, jouent un rôle particulier en mathématiques elles ont
donc une place à part dans Scilab et sont stockées dans des variables non modifiables qui
commencent par le caractère %. Voici les plus utiles :
- %e,%pi sont assez explicites (sinon les taper dans Scilab pour obtenir leur
valeur).
- La constante %i représente le nombre complexe i, en particulier
Scilab manipule les nombres complexes exactement comme les nombres réels.
- %eps représente le “zéro machine”, en particulier %eps donne l’ordre de
grandeur des erreurs d’arrondis dans les calculs en nombres flottants.
- %inf représente “l’infini machine” : toute valeur trop grande (grosso-modo plus
grande que 10300) est considérée comme ayant la valeur %inf (infini).
- Quand un résultat ne peut être interprété Scilab renvoie %nan qui signifie
“Not A Number”.
- Enfin les deux valeurs “Vrai” et “faux” sont deux constantes définies en
Scilab par %T et %F (voir plus loin la partie sur les booléens)
-->(1+%i)^2 ans = 2.i -->%eps %eps = 2.220E-16
-->(10^(160))^2 ans = Inf -->%inf*0 ans = Nan
|
|
3 Les variables
Pour simplifier la manipulation des nombres nous allons utiliser des variables. Une
variable est déterminée par un nom composé d’une suite d’au plus 24 caractères d’abord
une lettre éventuellement suivit d’autres lettres, de chiffres, ou de caractères spéciaux
comme _ mais différent des opérateurs déjà définis par Scilab : +*/^[](){}'&|~ .
L’affectation d’une valeur (réelle, complexe, booléenne ou autre) dans une variable se fait
en utilisant =. Si le résultat de la dernière opération n’a pas été stocké dans une variable
spécifique alors il est stocké dans la variable ans :
-->a=1+%i;b=sqrt(2); c=a/b c = .7071068 + .7071068i -->d=%f d = F
-->a*b ans = 1.4142136 + 1.4142136i -->ans ans = 1.4142136 + 1.4142136i
|
|
-
![[dangerous l bend]](xsok0c7f.png) Il n’y a donc pas de déclaration préalable des variables en Scilab, celle-ci
sont crées lors de l’affectation. La notion de type d’une variable (constant,
string, function ...) est donc beaucoup moins rigide en Scilab que dans un
langage compilé. En particulier le type d’une variable donné peut changer d’une
affectation à l’autre ! Il n’y a donc pas de déclaration préalable des variables en Scilab, celle-ci
sont crées lors de l’affectation. La notion de type d’une variable (constant,
string, function ...) est donc beaucoup moins rigide en Scilab que dans un
langage compilé. En particulier le type d’une variable donné peut changer d’une
affectation à l’autre ! |
Si besoin on peut tester le type d’une variable avec la fonction typeof :
-->a,typeof(a) a = 1. + i ans = constant -->d,typeof(d)
d = F ans = boolean
|
|
Plusieurs commandes permettent de connaître la liste des variables utilisées dans un
session Scilab . La commande who va lister tous les noms des variables de l’environnement
Scilab . On pourra ainsi se rendre compte que Scilab travaille avec de nombreuses
variables d’environnements (chemins vers des répertoires particuliers, noms de librairies,
constantes particulières,. . .). La commande whos -type permet de spécifier le type de
variable qu’on veut lister, et donc de clarifier quelque peut l’affichage. Enfin, à partir des
versions 5 de Scilab , il existe une fonction who_user qui ne liste que les variables définies
par l’utilisateur.
-->who
your variables are...
ans whos d c b a
scicos_pal %scicos_menu %scicos_short
%scicos_help %scicos_display_mode
modelica_libs scicos_pal_libs %helps WSCI
home SCIHOME PWD TMPDIR MSDOS SCI
guilib sparselib xdesslib percentlib
polylib intlib elemlib utillib statslib alglib
siglib optlib autolib roblib soundlib metalib
armalib tkscilib tdcslib s2flib mtlblib %F
%T %z %s %nan %inf COMPILER
%gtk %gui %pvm %tk $ %t
%f %eps %io %i %e
using 18185 elements out of 5000000.
and 71 variables out of 9231
your global variables are...
LANGUAGE %helps demolist %browsehelp LCC
%toolboxes %toolboxes_dir
using 1174 elements out of 11000.
and 7 variables out of 767
-->whos -type constant
Name Type Size Bytes
c constant 1 by 1 32
b constant 1 by 1 24
a constant 1 by 1 32
%scicos_display_mode constant 1 by 1 24
%nan constant 1 by 1 24
%inf constant 1 by 1 24
%eps constant 1 by 1 24
%io constant 1 by 2 32
%i constant 1 by 1 32
4 Les matrices
Il s’agit de la structure de données la plus importante dans Scilab , elle sera
constamment utilisée. Scilab permet de construire toutes sortes de matrices, à partir
des réels, mais aussi en utilisant des booléens, des chaînes de caractères . . .on
peut ensuite effectuer toutes les opérations algébriques usuelles définies sur les
matrices.
Il y a plusieurs manières de définir une matrice. La plus simple consiste à saisir la liste
des coefficients d’une matrice ligne par ligne, les lignes étant séparées par des
points-virgules, en utilisant l’opérateur de concaténation [ ] :
-->A=[1 2 3; 4 5 6; 7 8 9] A = 1. 2. 3. 4. 5. 6. 7. 8. 9.
--> B=[-1 0; 0 1; -3 0] B = - 1. 0. 0. 1. - 3. 0.
|
|
On peut accéder aux valeurs stockées dans une matrice en utilisant l’opérateur
d’extraction (). Pour récupérer (resp. modifier) la valeur en position i,j de la matrice A
il suffit d’appeler la commande A(i,j) (resp. A(i,j)=) sauf pour la matrice vide [] et
éventuellement les matrices à une ligne ou une colonne :
-->C=[]//matrice vide ans = [] -->A(1,2) ans =
2. -->A(1,2)=-2 A = 1. - 2. 3. 4. 5. 6.
7. 8. 9. -->L=[1 2 3]//la matrice ligne L = 1. 2. 3.
-->L(1,3)//accès normal ans = 3. -->L(2)//accès simplifié
ans = 2. -->L(2)=[]//supprimer L = 1. 3.
|
|
-
![[dangerous l bend]](xsok0c7f.png) Il ne faut pas confondre la syntaxe de Scilab avec celle d’autres langages (C
par exemple). Dans la gestion des matrices, en particulier, il ne faut pas confondre
les opérateurs [] et (). Une erreur très fréquente consiste à écrire A[1][2] au lieu
de A(1,2) ou L[2] au lieu de L(2). Il ne faut pas confondre la syntaxe de Scilab avec celle d’autres langages (C
par exemple). Dans la gestion des matrices, en particulier, il ne faut pas confondre
les opérateurs [] et (). Une erreur très fréquente consiste à écrire A[1][2] au lieu
de A(1,2) ou L[2] au lieu de L(2). |
Lorsqu’on modifie un coefficient qui “déborde” de la matrice de départ la matrice est
augmenté du nombre de lignes et de colonnes nécessaires et les cases correspondantes sont
mises à 0 :
-->C=[1 2 3; 4 5 6; 7 8 9] C = 1. 2. 3. 4. 5. 6.
7. 8. 9. -->C(5,4)=10 C = 1. 2. 3. 0.
4. 5. 6. 0. 7. 8. 9. 0. 0. 0. 0. 0.
0. 0. 0. 10.
|
|
Pour de petites matrices on rentrera tous les coefficients un à un comme ci-dessus mais
pour des matrices plus importantes il est utile de pouvoir les construire plus ou moins
automatiquement. On peut utiliser pour cela l’opérateur d’incrémentation :. Par exemple
pour construire une matrice à une ligne contenant les entiers de a à b on écrira
[a :b], si on veut spécifier un pas différent de 1 on pourra écrire [a :pas :b] avec
pas adapté (2 pour aller de 2 en 2 ou -1 pour diminuer de 1 à chaque pas) :
-->L1=[1:5] L1 = 1. 2. 3. 4. 5. -->L2=[7:2:15]
L2 = 7. 9. 11. 13. 15. -->L=[10:-1:5] L =
10. 9. 8. 7. 6. 5. -->L=[10:-2:20] L = []
|
|
On peut ensuite construire d’autres matrices à partir des précédentes par concaténation
-->[L1, L2]//on place L1 à gauche de L2
ans =
1. 2. 3. 4. 5. 7. 9. 11. 13. 15.
-->[L1; L2]//on place L1 au-dessus de L2
ans =
1. 2. 3. 4. 5.
7. 9. 11. 13. 15.
mais il faut faire attention aux tailles des matrices utilisées :
-->[A, B] //juxtaposer A puis B ans = 1. 2. 3. - 1. 0.
4. 5. 6. 0. 1. 7. 8. 9. - 3. 0.
-->[A;B]//pour mettre B sous A !--error 6 inconsistent row/column dimensions
-->[B,A]//juxtaposer B puis A ans = - 1. 0. 1. 2. 3.
0. 1. 4. 5. 6. - 3. 0. 7. 8. 9.
|
|
Il existe aussi des fonctions permettant de créer des matrices de tailles (p,n) déjà
remplies :
|
|
|
|
|
| matrice vide | matrice nulle | matrice identité | matrice de 1 | matrice aléatoire |
|
|
|
|
|
| [] | zeros(p,n) | eye(p,n) | ones(p,n) | rand(p,n) |
|
|
|
|
|
| |
On peut aussi appliquer ces différentes fonctions à des matrices déjà existante pour obtenir
une matrice de même taille (essayer zeros(A), zeros(B)).
-->zeros(4,3) ans = 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. -->ones(2,3) ans =
1. 1. 1. 1. 1. 1. -->eye(3,3) ans = 1. 0. 0.
0. 1. 0. 0. 0. 1. -->rand(3,2) ans =
0.9488184 0.7340941 0.3435337 0.2615761 0.3760119 0.4993494
|
|
La syntaxe des opérations matricielles est plus compliquée que pour les nombres flottants.
En effet il faut distinguer
- les opérations “terme à terme” qui s’appliquent à des matrices de même taille
- les opérations matricielles pour lesquelles les tailles des matrices en présence
doivent vérifier certaines conditions,
- les opérations qui combinent une matrice et un nombre
Commençons par les opérations terme à terme (par ordre de priorité croissante) :
|
|
|
|
|
| addition | soustraction | multiplication | division | puissance |
|
|
|
|
|
| + | - | .* | ./ | .ˆ |
|
|
|
|
|
| |
-->A+A ans = 2. - 4. 6. 8. 10. 12.
14. 16. 18. -->A-A ans = 0. 0. 0. 0. 0. 0.
0. 0. 0. -->A./A ans = 1. 1. 1. 1. 1. 1.
1. 1. 1. -->A.*A ans = 1. 4. 9. 16. 25. 36.
49. 64. 81. -->A.^2 ans = 1. 4. 9. 16. 25. 36.
49. 64. 81. -->A.^A ans = 1. 0.25 27.
256. 3125. 46656. 823543. 16777216. 3.874D+08
|
|
à ne pas mélanger avec les opérations purement matricielles (par ordre de priorité
croissante) :
|
|
|
|
|
| produit | division | puissance | transposition | conjugaison |
|
|
|
|
|
| * | / | ^ | .’ | ’ |
|
|
|
|
|
| |
-->A*B//produit matriciel ans = - 10. - 2. - 22. 5. - 34. 8.
-->B.'//transposée ans = - 1. 0. - 3. 0. 1. 0. -->A*A ans =
14. 12. 18. 66. 65. 96. 102. 98. 150. -->A^2
ans = 14. 12. 18. 66. 65. 96. 102. 98. 150.
|
|
il faut donc faire attention à ce que les tailles des matrices soient compatibles entre elles,
sinon on obtiendra un message d’erreur :
-->A+B !--error 8 inconsistent addition -->B*A !--error 10
inconsistent multiplication
|
|
sauf dans le cas où l’une des matrices est de taille 1 × 1 auquel cas on fera une opération
terme à terme entre un nombre et une matrice :
|
|
|
| addition | soustraction | multiplication |
|
|
|
| + | - | * |
|
|
|
| |
-->A A = 1. - 2. 3. 4. 5. 6. 7. 8. 9. -->1+A
ans = 2. - 1. 4. 5. 6. 7. 8. 9. 10. -->2-A
ans = 1. 4. - 1. - 2. - 3. - 4. - 5. - 6. - 7. -->3*A
ans = 3. - 6. 9. 12. 15. 18. 21. 24. 27.
|
|
Il faudra faire attention aux confusions possibles entre les différentes opérations
matricielles, termes à termes ou scalaire. En particulier le cas des divisions matricielles
peuvent conduire à des erreurs complexes :
-
![[dangerous l bend]](xsok0c7f.png) lorsqu’on veut faire une division terme à terme d’un réel par une matrice il
faut faire attention à la position du point du ./, s’il touche le réel à diviser le
point sera ignoré : 1./A donne la même chose que 1/A mais pas que (1)./A . Pour
une matrice A carrée 1/A est en fait l’inverse de la matrice (si il existe) qu’on peut
aussi obtenir par inv(A) ou A^(-1) . lorsqu’on veut faire une division terme à terme d’un réel par une matrice il
faut faire attention à la position du point du ./, s’il touche le réel à diviser le
point sera ignoré : 1./A donne la même chose que 1/A mais pas que (1)./A . Pour
une matrice A carrée 1/A est en fait l’inverse de la matrice (si il existe) qu’on peut
aussi obtenir par inv(A) ou A^(-1) . |
On peut vérifier la différence sur l’exemple suivant :
-->1./A ans = 0.125 - 1.75 1.125 - 0.25 0.5 - 0.25
0.125 0.9166667 - 0.5416667 -->(1)./A ans = 1. - 0.5 0.3333333
0.25 0.2 0.1666667 0.1428571 0.125 0.1111111
|
|
Pour les calculs d’inverse (qui peut ne pas exister dans certains cas) on obtient le même
résultat qu’avec 1/A
-->A^(-1) ans = 0.125 - 1.75 1.125 - 0.25 0.5 - 0.25
0.125 0.9166667 - 0.5416667 -->inv(A) ans = 0.125 - 1.75 1.125
- 0.25 0.5 - 0.25 0.125 0.9166667 - 0.5416667
|
|
Enfin, quand on a une matrice A de taille inconnue on peut récupérer le nombre de lignes
et/ou de colonnes par les instructions size(A),size(A,1),size(A,2). On peut aussi
utiliser length() quand la matrice a une seule ligne ou une seule colonne pour récupérer
sa longueur.
-->size(A) ans = 3. 3. -->size(B) ans = 3. 2.
-->size(C) ans = 5. 4. -->size(C,1) ans = 5. -->size(C,2) ans =
4. -->size(L1) ans = 1. 5. -->length(L1) ans = 5.
|
|
Il existe beaucoup de fonctions Scilab utiles pour les matrices : sum pour faire la somme
des coefficients d’une matrice, prod pour le produit , min et max pour trouver le coefficient
le plus petit/le plus grand d’une matrice . . .
-->A A = 1. - 2. 3. 4. 5. 6. 7. 8. 9.
-->sum(A) ans = 41. -->max(A) ans = 9.
|
|
En général, lorsqu’on applique une fonction de 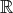 dans
dans 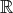 à une matrice elle est appliquée
à chaque terme de la matrice. cependant certaines fonctions courantes possèdent une
définition matricielle que ne correspond pas simplement à l’application de la fonction à
chaque terme de la matrice. Dans Scilab les versions matricielles des fonctions réelles sont
désignées par le même nom avec un m en plus à la fin. Par exemple pour la fonction
exponentielle :
à une matrice elle est appliquée
à chaque terme de la matrice. cependant certaines fonctions courantes possèdent une
définition matricielle que ne correspond pas simplement à l’application de la fonction à
chaque terme de la matrice. Dans Scilab les versions matricielles des fonctions réelles sont
désignées par le même nom avec un m en plus à la fin. Par exemple pour la fonction
exponentielle :
-->exp(A)//application terme à terme
ans =
2.7182818 0.1353353 20.085537
54.59815 148.41316 403.42879
1096.6332 2980.958 8103.0839
-->expm(A)//exponentielle de matrice
ans =
185820.61 178590.07 270297.43
988276.19 949854.08 1437565.7
1527664.9 1468268.9 2222171.
5 Les Booléens
Scilab permet aussi d’effectuer les principales opérations de comparaisons entre
nombres. Le résultat d’une telle opération est un booléen, Scilab reconnaît donc
aussi le type Booléen et effectue les opérations élémentaires associées. Les deux
valeurs “Vrai” et “Faux” sont deux constantes définies en Scilab par %T et %F
(ou %t,%f), le tableau ci-dessous donne les principaux opérateurs associées aux
booléens :
|
|
|
|
|
|
|
|
|
| égal | différent | inférieur | supérieur | inférieur | supérieur | ou | et | non |
| | | strict | strict | ou égal | ou égal | | | |
|
|
|
|
|
|
|
|
|
| == | <> | < | > | <= | >= | | | & | ~ |
|
|
|
|
|
|
|
|
|
| |
-
![[dangerous l bend]](xsok0c7f.png) Attention à ne pas confondre avec l’opérateur de comparaison == avec celui
d’affectation =. En particulier si on veut affecter un résultat de comparaison dans
une variable (booléenne) mieux vaut utiliser des parenthèses : Attention à ne pas confondre avec l’opérateur de comparaison == avec celui
d’affectation =. En particulier si on veut affecter un résultat de comparaison dans
une variable (booléenne) mieux vaut utiliser des parenthèses :
bool_faux=(1==2),bool_vrai=(1==1) |
Voici quelques exemples d’utilisation des booléens avec Scilab :
-->3<1 ans = F -->3=1//mauvaise comparaison Warning: obsolete use of =
instead of == ! ans = F -->3==1//bonne comparaison ans = F
-->%i^2==-1 ans = T -->~(3<1)&(%i^2==-1) ans = T -->%T|%F ans = T
|
|
On peut fabriquer des matrices de Booléens à partir de comparaisons directement
entre matrices de réels, la fonction find permet de trouver les cases de valeur vrai dans
une matrice Booléens :
-->x=rand(2,4)
x =
0.8782165 0.5608486 0.7263507 0.5442573
0.0683740 0.6623569 0.1985144 0.2320748
-->y=rand(2,4)
y =
0.2312237 0.8833888 0.3076091 0.2146008
0.2164633 0.6525135 0.9329616 0.312642
-->x<y
ans =
F T F F
T F T T
-->min(x)//minimum de x
m =
0.0683740
-->x==min(x)
ans =
F F F F
T F F F
-->[i,j]=find(x==min(x))//position du minimum
j =
1.
i =
2.
-->[i,j]=find(x==1)//un cas sans solution
j =
[]
i =
[]
6 Les chaînes de caractères
Scilab permet de manipuler facilement les chaînes de caractères, pour créer une chaîne
de caractères il suffit de la mettre entre apostrophes :
-->'une chaîne'
ans =
une chaîne
si on veut mettre une apostrophe dans une chaîne de caractères, il faudra la faire
précéder elle aussi d’une apostrophe :
-->txt='le caractère d''échappement est l''apostrophe'
txt =
le caractère d'échappement est l'apostrophe
On peut effectuer de nombreuses opérations sur les chaînes : concaténer deux chaînes par
+, calculer la longueur d’une chaîne par length() ou encore extraire le ke
élément d’une
chaîne avec part(chaîne,k) :
-->length(txt)
ans =
43.
-->part(txt,2)
ans =
e
-->'texte='+txt
ans =
texte=le caractère d'échappement est l'apostrophe
Chaque caractères possède un code numérique les fonctions str2code et code2str
permettent de passer de la chaîne au code et inversement. Par exemple le code de a est
10 et 11 est le code de b :
-->str2code('a'),code2str(11)
ans =
10.
ans =
b
-->logo='Scilab 5'
logo =
Scilab 5
-->str2code(logo).'
ans =
- 28. 12. 18. 21. 10. 11. 40. 5.
-->code2str(ans)
ans =
Scilab 5
-
![[dangerous l bend]](xsok0c7f.png) Les fonctions Scilab qui doivent traiter des fichiers externes (lecture/écriture
dans des fichiers textes en général) prennent en entré des noms de fichiers
représentés par des chaînes de caractères. Il faut donc bien penser à encadrer les
noms de fichiers par des apostrophes ! Les fonctions Scilab qui doivent traiter des fichiers externes (lecture/écriture
dans des fichiers textes en général) prennent en entré des noms de fichiers
représentés par des chaînes de caractères. Il faut donc bien penser à encadrer les
noms de fichiers par des apostrophes ! |
La conversion d’un résultat de calcul en chaîne de caractère se fait par la fonction
string, attention de ne pas confondre la chaîne affichée et la variable qu’elle représente :
-->%e//ne pas confondre le nombre
%e =
2.7182818
-->string(%e)//et la chaîne de caractères
ans =
2.7182818
-->%e==string(%e)
ans =
F
Lors de l’exécution de certains programmes il peut être utile de faire apparaître des
informations à l’écran, pour cela on peut utiliser la fonction disp :
-->u=%e-1
u =
1.7182818
-->disp(u)//affichage d'une variable
1.7182818
-->disp('u=%e-1='+string(u))//affichage d'un message
u=%e-1=1.7182818
-->disp(u,'u=%e-1=')//plus complexe
u=%e-1=
1.7182818
On peut faire appel à d’autres foncions pour afficher des résultats à l’écran,
Par exemple la fonction C printf peut être appelée directement dans Scilab :
-->printf('la valeur de e est \n e= %f \n',%e)
la valeur de e est
e= 2.718282
-->printf('les premiers entiers naturels sont %d,%d,%d ...\n',0,1,2)
les premiers entiers naturels sont 0,1,2 ...
On peut aussi fabriquer des matrices de chaînes de caractère dans un fichier avec les
commandes write ou mputl et les lire avec read ou mgetl :
-->M=['anglais' 'hello'; -->'français' 'bonjour'; -->'espagnol' 'hola'] M =
!anglais hello ! ! ! !français bonjour ! ! !
!espagnol hola ! -->mputl(M,'essai.txt') -->mgetl('essai.txt') ans =
! anglais ! ! ! ! français ! ! ! ! espagnol !
! ! ! hello ! ! ! ! bonjour ! ! ! ! hola !
|
|
Attention mputl permet de récrire sur un fichier ce que ne permet pas write :
-->mputl(M,'essai.txt')
-->mputl(M,'essai.txt')//réécriture sur le fichier
-->write('essai.txt',M)//réécriture sur le fichier
!--error 240
File essai.txt already exists or directory write access denied
7 Les fonctions
Un des concepts mathématique les plus important en informatique est le concept de
fonction. Scilab possède un type de variable function spécifique pour coder les fonctions,
d’ailleurs toutes les commandes que nous avons vu jusqu’ici sont en fait des fonctions
Scilab .
D’un point de vue mathématique, une fonction est une relation qui à un paramètre
d’entré associe au plus une valeur en sortie :
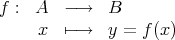 la
définition d’une fonction dans Scilab reprend exactement ce schéma mais sans contrôler
le type des variables en entrée/sortie (normal, puisque l’on ne déclare pas les types des
variables avant affectation). Par exemple, la fonction de
la
définition d’une fonction dans Scilab reprend exactement ce schéma mais sans contrôler
le type des variables en entrée/sortie (normal, puisque l’on ne déclare pas les types des
variables avant affectation). Par exemple, la fonction de 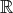 dans
dans 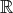 définie par
f(x) = 1 + x2 sera codée en Scilab par :
définie par
f(x) = 1 + x2 sera codée en Scilab par :
function [y]=f(x)
y=1+x^2
endfunction
|
-
![[dangerous l bend]](xsok0c7f.png) c’est « [y]= » qui indique la variable contenant le
résultats de la fonction, et pas « return y » en fin de
fonction, comme dans d’autres langages ! c’est « [y]= » qui indique la variable contenant le
résultats de la fonction, et pas « return y » en fin de
fonction, comme dans d’autres langages ! |
|
|
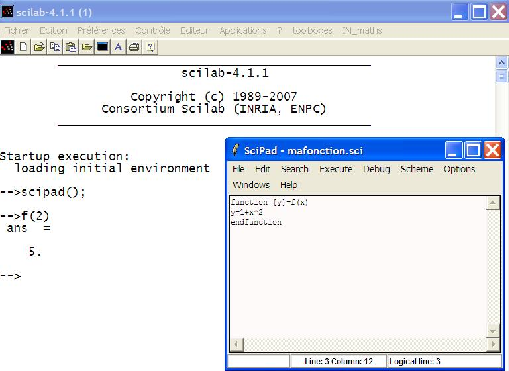
Maintenant il faut sauver ce code dans un fichier (appelons le mafonction.sci) et le
charger dans la session Scilab pour pouvoir ensuite l’utiliser. On peut pour cela utiliser
n’importe quel éditeur de texte, mais Scilab possède un éditeur de texte, scipad,
parfaitement adapté au langage Scilab (coloration syntaxique, numérotation des lignes,
recherche de mots, interfaçage avec Scilab, débogage . . .). Pour lancer Scipad
- cliquez sur l’onglet Editeur de la barre de menus
- dans la console utiliser la commande scipad()
une nouvelle fenêtre va s’ouvrir : c’est l’éditeur de texte que vous pouvez utiliser pour saisir le
code de la fonction f.
-
![[dangerous l bend]](xsok0c7f.png) Lorsqu’on veut enregistrer des définitions de fonctions Scilab dans un fichier
on lui donnera un nom de la forme *.sci, c’est à dire avec l’extension sci. Par
contre si on veut sauvegarder dans un fichier une liste de commandes à exécuter
séquentiellement (c’est à dire un script) on utilisera plutôt un nom de fichier avec
l’extension sce. Lorsqu’on veut enregistrer des définitions de fonctions Scilab dans un fichier
on lui donnera un nom de la forme *.sci, c’est à dire avec l’extension sci. Par
contre si on veut sauvegarder dans un fichier une liste de commandes à exécuter
séquentiellement (c’est à dire un script) on utilisera plutôt un nom de fichier avec
l’extension sce. |
On peut écrire plusieurs définitions de fonctions dans un même fichier. Une fois le
fichier sauvé on peut le charger dans Scilab depuis le menu execute de scipad (cf figure
FIG.4) ou avec la commande exec depuis la console. Une fois chargée, on peut utiliser
la fonction comme les autres fonctions Scilab . On peut aussi avoir besoin de
définir une fonction en une seule ligne avec la commande, c’est possible avec la
commande deff, mais moins maniable qu’avec la commande function (il faut une
certaines compréhension des problèmes liés aux chaînes de caractères dans ce cas).
-->exec('mafonction.sci')//définition via un fichier
-->deff('[y]=f(x)','y=1+x^2')//définition en ligne
-->f(2)
ans =
5.
-->whos -type function
Name Type Size Bytes
whos function 8512
f function 216
-->f(x)
f(x)
!--error 4
undefined variable : x
at line 5 of exec file called by :
exec('fonction.sce',1)
l’erreur générée à la dernière ligne ci-dessus impose une remarque importante
-
![[dangerous l bend]](xsok0c7f.png) Scilab est un logiciel de calcul numérique et pas un logiciel de calcul formel,
la commande f(x) n’a aucun sens si x n’est pas une variable définie (x=2 ou une
matrice par exemple). De même les commandes du type f(x)=1+x^2 ne définissent
pas une fonction Scilab . Scilab est un logiciel de calcul numérique et pas un logiciel de calcul formel,
la commande f(x) n’a aucun sens si x n’est pas une variable définie (x=2 ou une
matrice par exemple). De même les commandes du type f(x)=1+x^2 ne définissent
pas une fonction Scilab . |
Si on veut appliquer cette fonction f à une matrice il faut se méfier des confusions
entre opérations terme à terme et opérations matricielles. Par exemple, si x est une
matrice carrée x^2 sera interprété comme un produit matriciel et non comme
une élévation au carré de chaque terme. pour éviter ce genre de problèmes on
utilisera la commande feval pour évaluer une fonction sur chaque valeur d’une
matrice :
-->A=[1 2; 3 4] A = 1. 2. 3. 4. -->f(A) ans =
8. 11. 16. 23. -->1+A.^2 ans = 2. 5.
10. 17. -->feval(A,f) ans = 2. 5. 10. 17.
|
|
Cependant, en mathématiques, on peut considérer que les ensembles de départ et d’arrivé
d’une fonction sont en fait des produits d’ensembles. Ce point de vue est valable
dans Scilab ce qui permet de considérer facilement des fonctions ayant plusieurs
variables en entrée et en sortie contrairement à d’autre langages (comme le
langage C). Mais il faudra faire attention à bien récupérer les paramètres en
sortie :
function [a,b]=f(x,y) a=x+y b=x*y endfunction -->[a,b]=f(2,3) b =
6. a = 5. -->//b est perdue! -->f(2,3) ans = 5.
|
|
-
![[dangerous l bend]](xsok0c7f.png) lorsqu’une fonction renvoie plusieurs valeurs en sortie, il faut impérativement
récupérer chacune de ces valeurs dans des variables en suivant la syntaxe d’appel
donné dans la première ligne de la fonction : lorsqu’une fonction renvoie plusieurs valeurs en sortie, il faut impérativement
récupérer chacune de ces valeurs dans des variables en suivant la syntaxe d’appel
donné dans la première ligne de la fonction :
function [y1,y2,y3]=nomfonction(x1,x2,x3)
sinon seul le résultat y1 sera affiché. les autres résultats du calcul seront perdus ! |
Pour bien utiliser les fonctions Scilab il faut aussi comprendre le problème des
variables locales et des variables globales. Le mécanisme d’appel de fonction en conçu
pour que les variables définies à l’intérieur du corps de la fonction n’interfèrent pas avec
celle définies dans la session Scilab qui appelle la fonction.
-->a=1,b=2
a =
1.
b =
2.
-->deff('[a,b]=g(x)','a=x+1,b=2*b')
Warning :redefining function: g
-->[u,v]=g(3)//les valeurs de a et b sont prisent en compte
v =
4.
u =
4.
-->a,b//mais elles ne sont pas modifiée dans l'environnement global
a =
1.
b =
2.
On retiendra la règle suivante :
-
![[dangerous l bend]](xsok0c7f.png) Lors de l’appel à une fonction, si une variable apparaissant dans le corps
de la fonction n’est pas définie dans l’environnement local (entre les commandes
function et endfunction) alors pour évaluer cette variable Scilab va chercher si
cette variable est définie dans la session d’où la fonction a été appelée (ce qu’on
appelle l’environnement global). Si la variable n’est pas définie dans l’environnement
global il y aura une erreur avec le message undefined variable. Lors de l’appel à une fonction, si une variable apparaissant dans le corps
de la fonction n’est pas définie dans l’environnement local (entre les commandes
function et endfunction) alors pour évaluer cette variable Scilab va chercher si
cette variable est définie dans la session d’où la fonction a été appelée (ce qu’on
appelle l’environnement global). Si la variable n’est pas définie dans l’environnement
global il y aura une erreur avec le message undefined variable. |
Autant que faire se peut, on évitera d’utiliser dans le corps d’une fonction
des variables qui ne sont pas définies dans le corps de la fonction. si toute fois
on a besoin d’utiliser des variables globales on pourra utiliser la commande
global pour partager des variables entre plusieurs fonctions et l’environnement
global.
8 Programmation
Toutes les commandes vues depuis le début de ce chapitre forment les instructions de
base du langage de programmation de Scilab . Mais pour aller plus loin il nous manque
les instructions de base de l’algorithme que sont les branchements conditionnels et les
boucles.
|
|
| pseudo-code | scilab
|
|
|
|
|
| | |
|
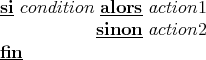 |
if condition then action1
else action2
end
|
|
|
|
|
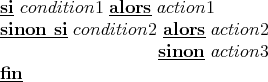 |
if condition1 then action1
elseif condition2 then action2
else action3
end
|
|
|
|
|
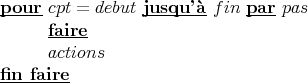 |
for cpt=debut:pas:fin
actions
end
|
|
|
|
|
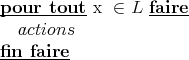 |
|
|
|
|
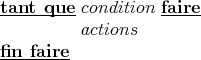 |
while condition
actions
end
|
|
|
|
|
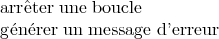 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
Dans ce qui précède condition représente une expression dont l’évaluation conduit
à une valeur booléenne (%t ou %f) et les action* représentent des suites de
commandes Scilab à exécuter suivant le cas. La syntaxe de la boucle for mérite une
explication particulière. En effet la syntaxe debut:pas:fin est exactement celle pour
créer une matrice ligne dont les valeurs partent de debut pour arriver à fin par
incrément de pas. On peut donc écrire les boucle for cpt=debut:pas:fin sous la
forme :
L=debut:pas:fin
for cpt=L
le compteur cpt prendra alors successivement toutes les valeurs de L (dans l’ordre).
Cette remarque est très utile pour réécrire certaines boucles plus simplement, en
particulier dans des structure algorithmique de type pour tout , pour chaque .
-
![[dangerous l bend]](xsok0c7f.png) Dans une structure conditionnelle l’instruction then peut être omise, mais
si ce n’est pas le cas alors les instructions if et then doivent obligatoirement
être sur la même ligne et il doit y avoir un espace avant le then. Dans une structure conditionnelle l’instruction then peut être omise, mais
si ce n’est pas le cas alors les instructions if et then doivent obligatoirement
être sur la même ligne et il doit y avoir un espace avant le then. |
Pour mieux comprendre prenons l’exemple très simple du calcul d’un factoriel. Si on
veut écrire un script pour calculer 10 ! en utilisant la définition n! = n× (n- 1)! et 1! = 1,
on écrira un fichier avec le code :
fact=1
for k=1:10
fact=k*fact
end
On sauve ce code dans un fichier script.sce que l’on peut exécuter dans Scilab avec la
commande exec(’script.sce’) ou en cliquant sur l’onglet execute-->load into
scilab de l’éditeur scipad.
-
![[dangerous l bend]](xsok0c7f.png) On évitera de lancer de lancer des instructions if, for, while
. . . directement dans la console et on privilégiera l’utilisation de fichiers (scripts).
En particulier lorsqu’une commande if, for ou while est lancée dans la console
aucune commande n’est exécutée tant que le end correspondant n’a pas été exécuté. On évitera de lancer de lancer des instructions if, for, while
. . . directement dans la console et on privilégiera l’utilisation de fichiers (scripts).
En particulier lorsqu’une commande if, for ou while est lancée dans la console
aucune commande n’est exécutée tant que le end correspondant n’a pas été exécuté. |
On peut aussi utiliser le langage de programmation Scilab à l’intérieur d’une
fonction Scilab . Par exemple pour la fonction définie par factoriel(n) = n! on
aura :
function [fact]=factoriel(n) fact=1 for k=1:n fact=k*fact end
endfunction -->factoriel(10) ans = 3628800.
|
|
On peut aussi utiliser la récursivité
function [fact]=factoriel(n) if n==0 then fact=1 else fact=n*fact(n-1)
end endfunction -->factoriel(10) ans = 3628800.
|
|
9 Sorties graphiques
Scilab possède une librairie graphique très puissante, qu’il n’est pas possible de
présenter entièrement ici. Pour pouvoir débuter avec Scilab il faut commencer par
comprendre comment tracer une courbe du plan comme le graphe d’une fonction par
exemple.
Pour tracer une courbe Scilab possède une fonction plot2d(x,y) qui va tracer une
ligne brisée en reliant par des segments de droites les points de coordonnées
(x(i),y(i)). Pour avoir un affichage convenable du graphe il faut donc avoir
suffisamment de points pour que la courbe est un aspect “lisse” et pas celui d’une ligne
brisée. La démarche est donc la suivante :
- découper l’intervalle en un nombre suffisant de valeurs rangées dans une
matrice colonne x
- calculer les valeurs correspondantes de f(x) (par exemple avec feval) et les
stocker dans une matrice colonne y
- exécuter la commande plot2d(x,y) pour ouvrir la fenêtre où s’affichera le
graphe
Pour améliorer l’aspect du graphe on pourra utiliser certaines options de la fonction plot2d
(voir l’aide en ligne pour plus de détails), par exemple :
- axesflag pour gérer le positionnement des axes,axesflag=5 pour avoir des
axes qui se croisent en (0, 0),
- frameflag pour gérer la taille de la fenêtre et les échelle,frameflag=4
pour une échelle isométrique, frameflag=6 pour avoir une échelle avec des
graduations “simples”,
- xgrid() permet d’afficher une grille pour lire les coordonnées,
- legends() permet d’afficher une légende,
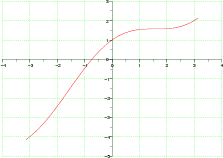
deff('y=f(x)','y=x+cos(x)')
x=[-%pi:0.01:%pi]';
y=feval(x,f);
plot2d(x,y,5,axesflag=5,frameflag=6)
xgrid(3)//grille verte
|
Quand on a plus besoin du graphe on peut détruire la fenêtre ou utiliser la commande
clf() pour effacer le contenu de la fenêtre. On peut aussi superposer des courbes en
exécutant plusieurs fois plot2d sans effacer la fenêtre ou en une seule commande comme
ci-dessous :
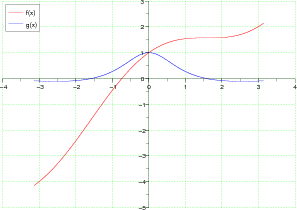
clf()//effacement de la fenêtre
deff('y=g(x)','y=cos(x)/(1+x^2)')
y2=feval(x,g);
plot2d([x x],[y y2],[5 2],axesflag=5,frameflag=6)
xgrid(3)
legends(['f(x)' 'g(x)'],[5 2],2)//affichage d'une légende
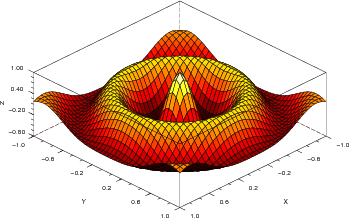
Pour les fonctions à deux variables on peut faire des graphiques en trois dimensions avec
plot3d1(x,y,z). Il faudra cette fois découper le domaine en petits rectangles (c’est à
dire découper l’intervalle des x et des y puis calculer les valeurs correspondantes de
z=f(x,y). Pour faciliter l’interprétation du graphe Scilab permet un affichage
des niveaux en couleur à l’aide d’une table des couleurs (colormap en anglais).
clf()
deff('z=f(x,y)','r=sqrt(x^2+y^2),z=exp(-r)*cos(3*%pi*r)')
x=[-1:0.01:1]';y=x;
z=feval(x,y,f);
cmap=hotcolormap(64);//table de 64 couleurs
xset("colormap",cmap);//chargement de la colormap
plot3d1(x,y,z)//affichage du graphe
![[dangerous l bend]](xsok0c7f.png) Ce document est conçu comme un recueil commenté d’exemples “simples” de
commandes Scilab . Il permet de découvrir l’existence de certaines commandes
Scilab et leur domaine d’utilisation, mais la lecture de ce document ne peut
remplacer la lecture de l’aide en ligne pour une utilisation optimale des commandes
décrites.
Ce document est conçu comme un recueil commenté d’exemples “simples” de
commandes Scilab . Il permet de découvrir l’existence de certaines commandes
Scilab et leur domaine d’utilisation, mais la lecture de ce document ne peut
remplacer la lecture de l’aide en ligne pour une utilisation optimale des commandes
décrites.  ), ce qui nous limite à une commande par ligne,
), ce qui nous limite à une commande par ligne,